We have our own technology called Neuron Machine (NM) architecture.
We opened the source code of hardware simulator here simulating an NM system computing deep belief networks.
Neuron Machine architecture
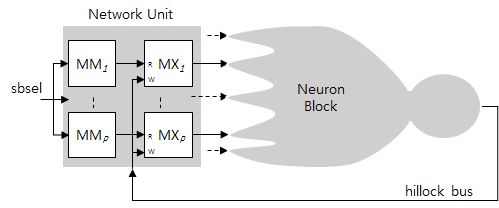
The NM is an innovative design paradigm for register-transfer (RTL) level, synchronous hardware systems. The NM system consists of a neuron block (NB) and a network unit (NU) as shown in the following figure.
In addition the overall system is controlled by a control unit (CU) which is not shown in this figure. The NB is essentially a single digital hardware neuron whose circuits reflect the computation of the various parts of model neuron. The NB consists of multiple, P, synapse units (SNUs), a dendrite unit (DU), and a soma unit (SU). The outputs of the SNUs are connected to the DU inputs, and the output of the DU is connected to the SU input. The inputs of the SNUs and the output of the SU become the inputs and output of the NB, and are connected to the outputs and input of the NU, respectively. All the units in the NB are designed into a large fine-grained pipelined circuit so that the overall NB can process P presynaptic inputs at every clock cycle and computes one neuron output at every bpn = [p/P] clock cycles, where p is the number of synapses on each neuron. The group of P synapses being computed together is called a synapse bunch (SB).
The NU is composed of P memory modules, each with two individual memories: MM and MX. In each memory module, the output of MM is connected to the address input of MX and the output of MX becomes one of P outputs of the NU. MXs are dual-port memories in which read and write operations can be carried out simultaneously. The write ports of all MX memories are connected together becoming the input of the NU. The contents of the kth MM and MX are:
- MMk(b) = mij
- MXk(a) = ya,
where i = mod(b × P + k, bpn × P), j = [b / bpn], mij is the index number of the neuron connected on the ith synapse of the jth neuron, and ya is the output of the ath neuron. By addressing all MM memories with an address b at the sbsel control input, the outputs of the presynaptic neurons connected to synapses in the bth SB are generated at the output of the NU, simultaneously storing the outputs of postsynaptic neurons through the input of the NU.
The CU repeats the same control sequences for each time step in which all presynaptic inputs for all neurons are supplied from the NU to the NB, starting from the first SB of the first neuron to the last SB to the last neuron. Simultaneously with the input flow, the outputs of postsynaptic neurons computed in the NB are sent to the NU via the axon bus.
The NM architecture have a number of advantages:
- Communication between the neurons is accomplished just by accessing memories requiring no communication overheads.
- Network topology information is stored only in MM memories with no restriction on the topology.
- State and parameter memories are distributed and embedded in the computational circuits and the data paths of the memories are short incurring no memory bottleneck problems.
- The speed does not depend on the firing rate as most event-driven implementations do.
- A large number of connections can be computed simultaneously by multiple SNUs.
- A large-scale pipelining parallelism can be obtained in the NB and the pipeline delay have little impact on the overall performance.
- Simple and uniform structure without necessarily requiring a main computer.
We published the NM architecture for multi-layer perceptron (MLP) in 2012 [1], and successfully applied to complex spiking neural networks [2] and back-propagation networks [3] in 2013. The NM architecture was further extended to support deep belief networks, in which computation procedure is highly complicated involving arbitrary number of restricted Boltzmann machines [4]. We believe the use of the NM architecture is not limited to neural network systems and it can be expanded to general high performance computing applications.
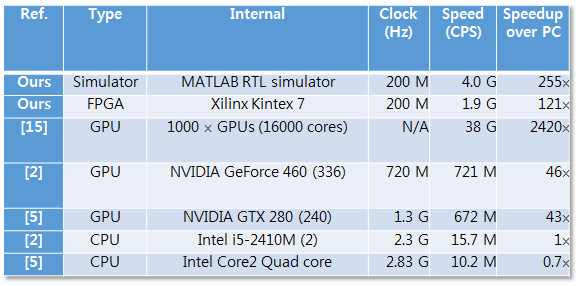
The resulting performances of the NM systems are astonishing. The our deep belief network system is compared with other systems in the following table.
Our small system using a mid-range FPGA chip outperformed most other CPU and GPU systems and only ten times slower than Google Brain system (third one) using 1000 GPUs!
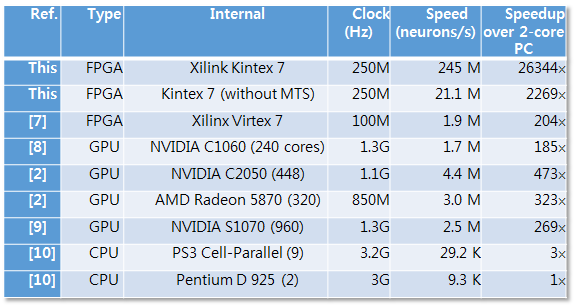
Our neuromorphic system is compared with other Hodgkin-Huxley neural systems. in the following.
Our Kintex 7 FPGA system showed more than 20000 times faster than a two-core PC and ten times faster than GPU systems.
References
[1] J. B. Ahn, “Neuron machine: Parallel and pipelined digital neurocomputing architecture,” in Computational Intelligence and Cybernetics (CyberneticsCom), 2012 IEEE International Conference on, 2012, pp. 143-147.
[2] J. B. Ahn, “Extension of neuron machine neurocomputing architecture for spiking neural networks,” presented at the International Joint Conference on Neural Networks (IJCNN2013), 2013.
[3] J. B. Ahn, “Computation of Backpropagation Learning Algorithm Using Neuron Machine Architecture,” in Computational Intelligence, Modelling and Simulation (CIMSim), 2013 Fifth International Conference on, 2013, pp. 23-28.
[4] J. B. Ahn, “Computation of Deep Belief Networks Using Special-Purpose Hardware Architecture,” International Joint Conference on Neural Networks (IJCNN2014), 2014.