1: NN require pre-determined arithmetic operations
Many neural network algorithms, including those for DBNs, require pre-determined arithmetic operations to complete the given job. For example, computation of one time step for typical recall-mode neural network, which can be described by following equation,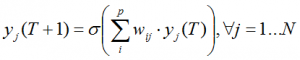 
requires N x p multiplications, N x (p – 1) additions, and N sigmoid functions, where N, p are the number of neurons in the network and the number of connections for each neuron, respectively. The same is true for ordinary DBN training algorithms. As the numbers of loops in the algorithms are independent of the data being computed, total number of arithmetic operations required to complete, say, a training epoch does not vary.
2: Computations only by arithmetic operators
In any computational system, arithmetic operations can be computed only by the hardware of arithmetic operators. In the typical CPUs, arithmetic operators reside in SIMD extension hardware such as SSE or AVX (in case of Intel CPUs). In the GPUs, arithmetic operators are in fused multiply-accumulators (FMAs) in each core. Arithmetic operators are the only way to handle arithmetic operations.
Formulation of performance-resource ratio
These two points indicate that in order to run the algorithm faster (1) you have to use arithmetic operators as much as possible, and (2) you have to utilize them as much time as possible. This leads to the formulation of performance-resource ratio as following equation.
R = Rc x Ru
where Rc is the proportion of resources (transistors) minimally required to implement the arithmetic operators over all hardware resources in the system, and Ru is the proportion of time the operators effectively produce outputs. The performance-resource ratio, R, becomes 100% when all hardware resources are used to implement most efficient arithmetic operators and all such arithmetic operators are utilized in full time producing effective outputs at all clock cycles. In theory, a 100% R is not possible because input data must be prepared and output data must be handled by the architecture in order to make arithmetic operators in operation.
How do CPUs and GPUs compute DBNs?
In a state-of-art DBN implementation, it took 40 min to train 60000 samples with a 784×800 RBM on an Intel dual-core i5-2410M 2.3-GHz CPU [2]. According to the RBM algorithms, the computation requires approximately 4 × 1011 arithmetic operations. In this CPU, computations are handled by one Advanced Vector Extensions (AVX) block contained in each core (two cores in the CPU), and each AVX can sustain four FP operations per clock cycle. Therefore, the full throughput of the CPU that can compute in 40 min is 4.4 × 1013 arithmetic operations. This estimation shows that the arithmetic operators effectively work for less than 1% of the full CPU time. The number of transistors used for the CPU is 6.24 × 108 [3], whereas an FP multiplier can be implemented using only 2 × 105 transistors [4]. Therefore,
R of CPU « 0.01% (Ru ≈ 1%, Rc « 1%).
In the case of a GPU, a 720-MHz NVIDIA GeForce 460, for example, has 336 cores each computing one FP fused multiply-add operation per cycle. A state-of-art RBM implementation on this GPU computed the same RBM computation 46 times faster than the CPU [2], which resulted in a similar operator utilization rate as PC. Number of transistors used for the GPU is 1.95 × 109 and it has 336 arithmetic operators. Assuming the number of transistors for one operator to be 2 x 105, total resource required for 336 operators becomes 6.72 x 107. Therefore,
R of GPU ≈ 0.035 % (Ru ≈ 1%, Rc ≈ 3.5 %).
Similar results on other CPUs and GPUs have been reported in [5, 6]. This means that conventional computers use only a small fraction of the time and resources for the computation. This shows the potential that a huge performance improvement might be achieved even using the same hardware resources.
The operator utilization of GPU (1%) can be depicted as following figure.
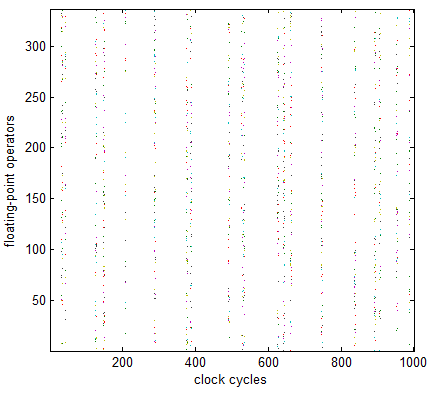
Utilization of 336 operators in GPU (simulated). Each colored dot denotes an active output of the respective arithmetic operator at a specific clock cycle.
The result of our system
Following figure is the footprint of the arithmetic operators in our system that was generated from this hardware simulator. Each colored dot in this figure
denotes an active output of the respective arithmetic operator at a specific clock cycle.
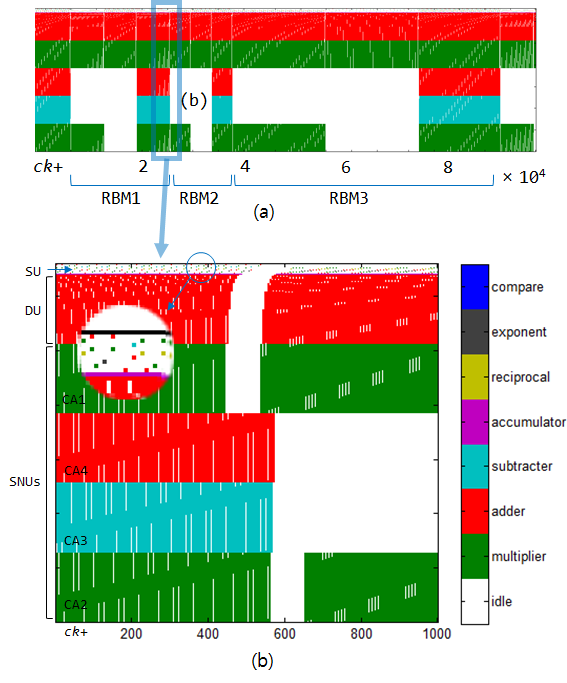
Footprint of 331 arithmetic operators generated from working source code (Simulation 3): (a) stages for one training sample, (b) detailed view.
A total of 331 operators in the system produced their outputs for 61.5% of the number of clock cycles on average throughout the computation. Therefore,
Ru of our system = 61.5%
According to our FPGA implementation, explained in the background section of this web site, the proportion of resources used for single-precision (SP) FP operators is approximately 73% over total resources used to build the system.
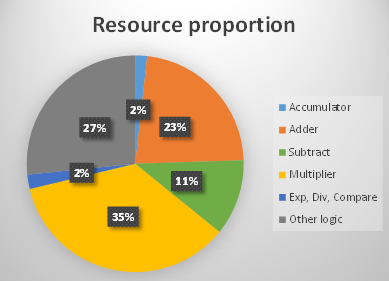
Resource proportion in our FPGA implementation
As we consider double-precision (DP) FP operators in the CPU and GPU cases, and a DP FP operator takes approximately four times more resources than an SP FP operator, even higher Rc than 73% would be expected in a DP Neuron Machine system. As the FPGA implementation is a prototype for ASIC system, similar resource composition rate could be achieved when we implement the same design on ASIC using the best arithmetic operator technologies. Therefore,
R of ASIC Neuron Machine > 45% (Ru ≈ 61.5%, Rc > 73%).
Please note that the CPUs and GPUs are general purpose computers and large part of their architecture are devoted to support the generality, that is, to compute any algorithms without changing hardware. The better performance-resource comparison here is meaningful only when the hardware is used dedicatedly for neural networks.